Department of Scientific Computing    Institute for Numerical Simulation    University of Bonn

Documentation

Download

Programming References

Bug Reports / Suggestions

FAQ

Authors

           

---

Matrix Class Template Reference

Matrix<class I,int DIM> is a general implementation of a DIM-dimensional array. Besides initialization, data access via iterators we provide some basic IO and linear algebra stuff (when I is a scalar type). More...

#include <Matrix.hpp>

List of all members.

Public Methods
	Matrix ()
	default constructor.
	Matrix (int *begin, int *end)
	constructor with initialization, see Init.
void	Init (int *begin, int *end)
	initializes *this with extent .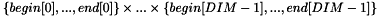
I&	operator[] (const iterator &it)
	access to data.
I&	operator[] (const int *in)
	access to data via multi-index.
iterator	begin () const
	get lower bound for iterator.
iterator	begin (int constcoordinate) const
	get lower bound for iterator with fixed coordinate direction, see Matrix::iterator.
iterator	end () const
	get upper bound.
int	size (const int i) const
	return number of components.
void	Print (int l=0)
	print, l=0 just dimension, l=1 and DIM=2 also the values.
void	Set (const I &i)
	set all components.
void	Set (Function *F)
	set with the values of the given function, the indices are translated to a multi-vector x \in [0,1]^DIM used as argument for *F.
void	Copy (Matrix< I, DIM > *X)
	copy the whole matrix.
void	Set (Matrix< I, DIM > *X)
	just copy for those indices which are in the intersection of the ranges of both matrices.
void	Abs (Matrix< I, DIM > *X)
	(*this)=Abs(*X) this and all other linear algebra operations are to be understood componentwise.
void	Pow (Matrix< I, DIM > *X, double p)
	(*this)=pow(*X, p).
void	Sqr (Matrix< I, DIM > *X)
	(*this)=pow(*X, 2).
void	PPlus (Matrix< I, DIM > *X)
	(*this) += *X.
void	PPlus (const double a, Matrix< I, DIM > *X)
	(*this) += a*(*X).
void	Add (Matrix< I, DIM > *X, Matrix< I, DIM > *Y)
	(*this) = (*X) + (*Y).
void	Add (const double a, Matrix< I, DIM > *X, const double b, Matrix< I, DIM > *Y)
	(*this) = a*(*X) + b*(*Y).
void	Add (const double a, Matrix< I, DIM > *X, const double b, Matrix< I, DIM > *Y, const double c, Matrix< I, DIM > *Z)
	(*this) = a*(*X) + b*(*Y) + c*(Z).
void	Add (const double a, Matrix< I, DIM > *X, const double b, Matrix< I, DIM > *Y, const double c, Matrix< I, DIM > *Z, const double d, Matrix< I, DIM > *Q)
	(*this) = a*(*X) + b*(*Y) + c*(Z) +d*(*Q).
void	Add (const double a, Matrix< I, DIM > *X, const double b, Matrix< I, DIM > *Y, const double c, Matrix< I, DIM > *Z, const double d, Matrix< I, DIM > *Q, const double f, Matrix< I, DIM > *R)
	(*this) = a*(*X) + b*(*Y) + c*(Z) +d*(*Q) +f*(R).
void	MMinus (Matrix< I, DIM > *X)
	(*this) -= *X.
void	MMinus (const double a, Matrix< I, DIM > *X)
	(*this) -= a*(*X).
void	Sub (Matrix< I, DIM > *X, Matrix< I, DIM > *Y)
	(*this) = (*X) - (*Y).
double	InnerProd (Matrix< I, DIM > *X)
	return the innerproduct of all components.
void	Mul (Matrix< I, DIM > *X, Matrix< I, DIM > *Y)
	(*this) = (*X) * (*Y).
void	Mul (Matrix< I, DIM > *X, Matrix< I, DIM > *Y, const double f)
	(*this) = (*X) * (*Y)*f.
void	Mul (Matrix< I, DIM > *X, const double f)
	(*this) = (*X) * f.
void	Mul (const double f)
	(*this) *= f.
void	Multiply (Matrix< I, DIM > *X, Matrix< I, DIM > *Y)
	Matrix-Matrix multiply of two compatible 2D matrices.
double	Min ()
	return the minimum of all components.
double	Max ()
	return the maximum of all components.
double	MaxAbs ()
	return the maximum of absolute values.
double	Sum ()
	return the sum of all components.
double	SumAbs ()
	return the sum of absolute components.
double	SumSqr ()
	return the sum of the squares of all components, i.e. InnerProd(this), but is faster.
void	Transpose (Matrix< I, DIM > *X)
	transpose.
void	WriteUDF (const char *filename, Extensions< DIM > *E, const char *ScalarOrVectorName, Matrix< I, DIM > **M, int NM, bool castfloat=false, bool ascii=false)
	write a file which can be read from VTK (vtkRectilinearGridReader) or in MATLAB using ReadUDF; do help ReadUDF for more MATLAB-information .
void	ReadUDF (const char *filename, Extensions< DIM > *E, const char *ScalarOrVectorComponentName)
	read from an UDF-file (unified data format) ScalarOrVectorComponentName not yet supported, for future compatibility.

template<class I, int DIM> class Matrix

---

The documentation for this class was generated from the following file:

• Matrix.hpp

---