PressureOperatorII Struct Template Reference

Consistent pressure Laplacian div*grad WITHOUT stabilized discretization.

For a particular face of the computational domain there are either periodic BC for pressure and velocity OR there are homogeneous Neumann BC for the pressure and no BC for the velocity.
The resulting Poisson problem is in any case singular. In order to improve the convergence to a particular (or an almost) solution one can augment the problem to a saddle point formulation of type

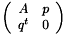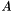is the singular operator and

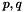are the augmention vectors. If

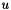and

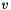are the right and left null vector of

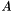, i.e.

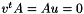, then

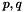must satisfy the following conditions:

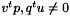. More...

#include <Operators.hpp>

Inheritance diagram for PressureOperatorII::

List of all members.

Public Methods
virtual void	Apply (I X, I Result)
	Apply returns R(Result) with respect to the boundary conditions of (X).
virtual void	Preconditioner (I X, I Result)
	if one wants to solve an operator equation with this operator, one can provide a preconditioner.
virtual void	InversePreconditioner (I X, I Result)
	the BiCGStab2 solver also needs the inverse operation.
virtual double	DiagonalEntry (int level, Wavelets W)
	often the DiagonalEntry is needed for preconditioners.
virtual void	NotUsing (I *X)
	the solvers check whether the temporary data used by them is also used for the evaluation of the operator; this is avoids wrong numerical results.

template<class I, int DIM> struct PressureOperatorII

The documentation for this struct was generated from the following file:

Operators.hpp

Generated at Mon Aug 19 10:02:33 2002 for AWFD by

PressureOperatorII Struct Template Reference

Public Methods

template<class I, int DIM> struct PressureOperatorII