Department of Scientific Computing    Institute for Numerical Simulation    University of Bonn

Documentation

Download

Programming References

Bug Reports / Suggestions

FAQ

Authors

           

---

UniformData Struct Template Reference

UniformData is a very simple data structure for uniform grids based on arrays.
Like the other data structures it additionally contains the Extensions<DIM>.
. More...

#include <UniformData.hpp>

List of all members.

Public Methods
	UniformData ()
	Default constructor.
	UniformData (int *begin, int *end, Wavelets *W, double *XA=NULL, double *XE=NULL)
	Constructor with initialization, see Init(.).
void	Init (int *begin, int *end, Wavelets *W, double *XA=NULL, double *XE=NULL)
	Initializes *this with extent 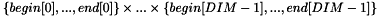. Furthermore, the Extensions are initialized with *W and *XA, *XE, see Extensions<DIM>.
void	SetBoundaryConditions (UniformData< DIM > *X)
	Copy boundary conditions from *X.
void	SetBoundaryConditions (int BC[DIM][2])
	Set boundary conditions.
void	SetBoundaryConditions (int dir, int *bc)
	Set boundary conditions with respect to coordinate direction dir.
void	SetBoundaryConditions (int dir, int bc0, int bc1)
	Set boundary conditions with respect to coordinate direction dir.
bool	SameBoundaryConditions (UniformData< DIM > *X)
	Return true if *this and *x have the same boundary conditions.
void	CopyExtensions (UniformData< DIM > *X)
	Copy just the Extensions.
void	SetFunction (Function *F, bool boundaryonly=false, bool notransform=false)
	Set (*this) as the interpolant of (*F) with respect to the given grid. You must set some valid boundary condition identifiers first, to define the periodic coordinate directions. The boundary conditions will be either 'no BC' or periodic. For the treatment of Dirichlet boundary conditions, *F should be as smooth as possible. If (boundaryonly==true) then a quite smooth extension of JUST the boundary values is computed. If notransform==false the nodal values are wavelet transformed, otherwise we keep the nodal represenation. In the later case, boundaryonly must be false.
double	Max ()
	Return maximum value.
double	Min ()
	Return minimum value.
double	MaxAbs ()
	Return maximum absolute value.
double	Sum ()
	Return sum of all entries.
double	SumAbs ()
	Return sum of absolute entries.
double	SumSqr ()
	Return sum of all squared entries.
double	LpNorm (UniformData< DIM > *Tmp, double p)
	Calculate (approximate) Lp-Norms via transform in physical space, pointwise evaluation of |.|^p transform back in wavelet space and exact integration of this interpolant. Requires auxiliary data structure, *Tmp==*this is valid, but then *this is altered. Use p==HUGE_VAL to get maximum norm.
double	LmaxNorm (UniformData< DIM > *Tmp)
	maximum norm.
double	L2Norm (UniformData< DIM > *Tmp)
	L^2 norm.
double	L1Norm (UniformData< DIM > *Tmp)
	L^1 norm.
double	Integrate ()
	Compute exact integral of *this.
double	InnerProd (UniformData< DIM > *X)
	Compute inner product of the entries of *this and *X.
void	Set (const double a)
	All entries are set to a.
void	Copy (UniformData< DIM > *X)
	Copy everything from *X.
void	Set (UniformData< DIM > *X)
	Just copy for those indices which are in the intersection of the ranges of both matrices.
void	Abs (UniformData< DIM > *X)
	Compute componentwise the absolute values.
void	Pow (UniformData< DIM > *X, double p)
	Compute componentwise the given power.
void	Sqr (UniformData< DIM > *X)
	Compute componentwise the square ( faster than pow(X,2) ).
void	PPlus (UniformData< DIM > *X)
	(*this) += (*X).
void	PPlus (const double a, UniformData< DIM > *X)
	(*this) += a*(*X).
void	Add (UniformData< DIM > *X, UniformData< DIM > *Y)
	(*this) = (*X)+(*Y).
void	Add (const double a, UniformData< DIM > *X, const double b, UniformData< DIM > *Y)
	(*this) = a*(*X) + b*(*Y).
void	Add (const double a, UniformData< DIM > *X, const double b, UniformData< DIM > *Y, const double c, UniformData< DIM > *Z)
	(*this) = a*(*X) + b*(*Y) + c*(Z).
void	Add (const double a, UniformData< DIM > *X, const double b, UniformData< DIM > *Y, const double c, UniformData< DIM > *Z, const double d, UniformData< DIM > *Q)
	(*this) = a*(*X) + b*(*Y) + c*(Z) +d*(Q).
void	Add (const double a, UniformData< DIM > *X, const double b, UniformData< DIM > *Y, const double c, UniformData< DIM > *Z, const double d, UniformData< DIM > *Q, const double f, UniformData< DIM > *R)
	(*this) = a*(*X) + b*(*Y) + c*(Z) +d*(Q) +e*(R).
void	MMinus (UniformData< DIM > *X)
	(*this) -= (*X).
void	MMinus (const double a, UniformData< DIM > *X)
	(*this) -= a*(*X).
void	Sub (UniformData< DIM > *X, UniformData< DIM > *Y)
	(*this) = (*X) - (*Y).
void	Mul (UniformData< DIM > *X, UniformData< DIM > *Y)
	(*this) = (*X) * (*Y) (componentwise).
void	Mul (UniformData< DIM > *X, UniformData< DIM > *Y, double f)
	(*this) = (*X) * (*Y) *f (componentwise).
void	Mul (UniformData< DIM > *X, double f)
	(*this) = f (*X).
void	Mul (double f)
	(*this) *= f.
void	ApplyOp (int *BCT, UniformData< DIM > *X, int dir, unsigned int op)
	apply operation with respect to one coordinate direction in contrast to AdaptiveData::ApplyOp finite difference operators don't require a multiscale representation of *X Parameters: X   argument for the operation; may be *this dir   coordinate direction with respect to which the operation is applied BCT   boundary conditions of test functions along the <dir>th coordinate direction and also the boundary conditions of *this after the operation w.r.t. <dir>. The resaon is that e.g. FIRTSDERIVATIVE and also finite difference operations are considered as projections of something onto a test space op   a valid operation-ID valid IDs are: NOOPERATION do nothing TRANSFORM wavelet transform INVERSETRANSFORM inverse transform INTERPOLET2LIFTING change of basis from Interpolets to Lifting-Interpolets LIFTING2INTERPOLET change of basis from FIRSTDERIVATIVE compute (Petrov-)Galerkin projection of first derivative, test functions are the dual wavelets, a finite difference approximation is used for low order Interpolets STIFFNESS as above, but second derivative PROJECTION just projection FD12 finite fifferences 1. derivative 2. order accuracy FD14 finite fifferences 1. derivative 4. order accuracy FD16 finite fifferences 1. derivative 6. order accuracy FD22 finite fifferences 2. derivative 2. order accuracy FD24 finite fifferences 2. derivative 4. order accuracy FD40 finite fifferences 4. derivative 0. order accuracy FD60 finite fifferences 6. derivative 0. order accuracy FD12II as above, but consistent treatment at interval bounds FD22II as above FD14II as above FD24II as above DIV stabilized div operator</td> GRAD stabilized div operator</td> DIVGRAD stabilized div-grad operator</td> DIVFD4 stabilized div operator with 4th order f.d. stencil DIVFD6 stabilized div operator with 6th order f.d. stencil GRADFD4 as above GRADFD6 as above DIVGRADFD6 as above DIVGRADFD4NOSTAB no stabilization WENO3 3rd order WENO finite difference scheme WENO5 5th order WENO finite difference scheme FFT fast Fourier transform IFFT fast inverse Fourier transform POLYQUAD polynomial exact qudrature for Daubechies scaling functions INVERSEPOLYQUAD inverse to above NODALQUAD just take the nodal values INVERSENODALQUAD inverse to above ONEPOINTQUAD nodal quadrature with simple boundary treatment for Daubechies scaling fs. INVERSEONEPOINTQUAD inverse to above SHORTQUAD polynomial at boundaries, one point at inner points, very fast and effective! INVERSESHORTQUAD inverse to above .
void	MRATransform (UniformData< DIM > *X)
	standard (Meyer-) multivariate wavelet transform.
void	MRAInverseTransform (UniformData< DIM > *X)
	standard (Meyer-) multivariate inverse wavelet transform.
void	FourierCoefficient (double *re, double *im, int *k)
	Access to Fouriercoefficients, where k: -N[i]/2 < k[i] <= N[i]/2, i=1..DIM. Direct access would be a little bit complicated because of the FFTW's storage scheme.
void	WriteUDF (const char *filename, UniformData< DIM > *Tmp=NULL, bool CastToFloat=false)
	Write a file which can be read by VTK (vtkRectilinearGridReader) or by MATLAB (ReadUDF); Do help ReadUDF for more MATLAB-information. The Extensions<DIM> are written. Parameters: Tmp   if Tmp!=NULL *this is transformed to nodal values (if necessary -- *Tmp is modified in this case --) and these are written to the file Tmp must point to an UniformData of the same size than *this, *Tmp may be the same as *this. CastToFloat   if true just write float values to save disk space.
void	ReadUDF (const char *name)
	Read a file. If necessary, the matrix is automatically resized. The Extensions<DIM> (boundary conditions, multiscale or not,...) are read (if the file contains these informations). Files generated in MATLAB do not contain these up to now!
void	ReadSparse (const char *name, int which=0)
	read component <which> from a file in sparse data format.
void	WriteSparse (const char *filename, UniformData< DIM > **M=NULL, int N=0, bool CastToFloat=false)
	write M[0],...,M[N-1] to a file in sparse data format, set CastToFloat=true to save disk space.
double&	operator[] (const class Matrix< double, DIM >::iterator &it)
	access via matrix iterator.
double&	operator[] (const int *in)
	access via multi index.

template<int DIM> struct UniformData

---

The documentation for this struct was generated from the following file:

• UniformData.hpp

---