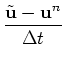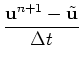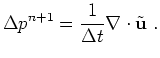The Projection-Method

NaSt3DGP employs a Chorin-type projection method for the decoupling of momentum and continuity equations. The general procedure for projection methods is a predictor-corrector approach. In a first step a preliminary velocity field is computed utilising the momentum equations. This velocity does not satisfy the continuity equation. In a second step a poisson-type equation for the pressure is solved which is derived using the continuity equation. In the last step the preliminary velocity field is projected onto a divergence-free velocity field using the computed pressure.

Neglecting the spatial discretization (for the time being) this procedure reads

1. Given ${\bf u}^n$, solve

$$\frac{\tilde{\bf u}-{\bf u}^n}{\Delta t} = {\bf g} -{\bf u}^n \cdot \nabla {\bf u}^n +\nu \Delta {\bf u}$$ (3.5)

2. Solve

$$\frac{{\bf u}^{n+1}-\tilde{\bf u}}{\Delta t} = -\nabla p^{n+1}$$ (3.6)

$$\nabla\cdot {\bf u}^{n+1} = 0~.$$ (3.7)

Application of the divergence operator to () leads to the Poisson equation for the pressure

$$\Delta p^{n+1}= \frac{1}{\Delta t} \nabla\cdot \tilde{\bf u}~.$$ (3.8)