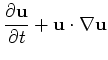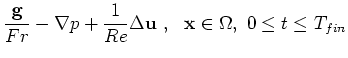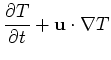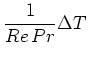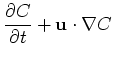Next: The Projection-Method Up: userguide Previous: Running a first example Contents
Numerical Method
In this chapter we give a brief description of the numerical method
underlying NaSt3DGP. For more information please refer to [1]. In several
cases, different numerical methods, for example, different
discretizations for time derivatives or convective terms, are
possible. Details on how to control these schemes using the scene
description file are given in section The basic mathematical model are the dimensionless time-dependent incompressible Navier-Stokes equations
subject to appropriate initial and boundary conditions. ![]() is the
dimensionless Reynolds-number which determines the ration between
inertia and viscous forces in the flow. the Reynolds-number is given
by
is the
dimensionless Reynolds-number which determines the ration between
inertia and viscous forces in the flow. the Reynolds-number is given
by
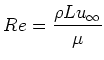
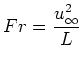
If thermal effects or the behaviour
of a scalar, driven by the flow, are of interest, (![]() ) and (
) and (![]() ) are completed
by equations for the energy (temperature) and the transport of a scalar
) are completed
by equations for the energy (temperature) and the transport of a scalar
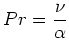
Subsections
- The Projection-Method
- The Boussinesq-Approximation
- Time discretization
- Boundary conditions
- Computational grid and spatial discretization
- Discretization of boundary conditions
Next: The Projection-Method Up: userguide Previous: Running a first example Contents Martin Engel 2004-03-15