Next: Navcalc and Navcalcmpi Up: Numerical Method Previous: Computational grid and spatial Contents
Discretization of boundary conditions
As described in [1], Dirichlet conditions for the velocity are implemented by setting the nodal value of the normal velocity component or by linear interpolation for the tangential velocity components. The homogeneous boundary Neumann conditions for the pressure are discretized by, e.g.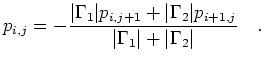
Martin Engel 2004-03-15
![\includegraphics[width=0.6\textwidth,keepaspectratio]{p3.eps}](img125.png)