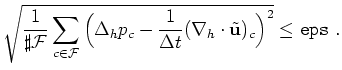All physical quantities, like Dirichlet values for the velocity, temperature or the viscosity
are assumed to be given in standard ISO units (m, s, kg, K and derived units), unless the
dimensionless-flag is set(see below).
Table:
List of entries in the parameter-block
| Name |
Type |
Default |
Description |
| |
|
|
|
| |
|
|
|
| Flow parameters |
| |
|
|
|
| Tfin |
double [s] |
1.0 |
defines the (physical) timespan of the simulation |
| reynolds |
double |
10.0 |
is the dimensionless Reynolds-number which describes the ratio
between inertia and viscous forces in the flow |
| nuC |
int |
0 |
the paramter nuC sets the number of species to be transported with the flow. For each species, a
diffusion constant has to be specified in a comma-separated list after nuC, i.e. the line has to look like
nuC
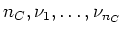 where where 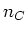 is an integer specifying the number of species and is an integer specifying the number of species and 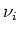 is a double value which stands for the diffusion parameter of the i-th species. You have to make sure that you also specify
initial conditions using the keyword cheminit. Details on how to specify initial and boundary conditions are given in
section
is a double value which stands for the diffusion parameter of the i-th species. You have to make sure that you also specify
initial conditions using the keyword cheminit. Details on how to specify initial and boundary conditions are given in
section ![[*]](file:/usr/share/latex2html/icons/crossref.png) |
| gx |
double [m/s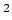 ] ] |
0.0 |
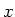 -component of external volume force -component of external volume force 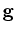 in ( in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) (or ) (or
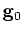 in ( in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) if the temperature is calculated). In the latter case ) if the temperature is calculated). In the latter case 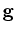 is computed from
is computed from 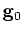 by means of ( by means of (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) ) |
| gy |
double [m/s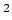 ] ] |
0.0 |
Same as gx for the 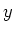 -component -component |
| gz |
double [m/s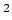 ] ] |
0.0 |
Same as gx for the 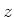 -component -component |
| froude |
double |
1.0 |
the Froude-number is a dimensionless number describing the ratio between
inertial and gravitational forces |
| beta |
double [1/K] |
1e-4 |
volume expansion coefficient in equation (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) ) |
| TempRef |
double [K] |
273.0 |
reference temperature in (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) ) |
| prandtl |
double |
1.0 |
the Prandtl-number is a dimensionless number describing the ratio between momentum and
heat transfer in the fluid |
| Timestep control |
| |
|
|
|
| deltmax |
double [s] |
1.0 |
upper bound for 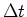 |
| tfconv |
double |
0.1 |
security factor for the timestep restriction arising from the convective terms.
In every step, 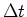 will be set less or equal than
where will be set less or equal than
where 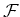 denotes the set of cells
in denotes the set of cells
in 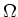 |
| tfdiff |
double |
0.2 |
security factor for the timestep-restriction arising from the diffusive terms.
In every step, 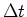 will be set less or equal than will be set less or equal than
and
 |
| Data output |
| |
|
|
|
| prstep |
int |
20 |
defines when to write the computed values to the binary file. Each prstep-th
timestep the current solution is written to the binary file(the file is overwritten) |
| TimePrintStep |
string |
- |
defines an interval (in physical time) after which the solution should be written to files
in a directory specified by TargetDirectory.
If TimePrintStep is not specified, no output will be generated. |
| TargetDirectory |
string |
- |
specifies the directory(absolut pathname) where the files
generated by TimePrintStep should be stored |
| Parameters controlling numerical methods |
| |
|
|
|
| TimeDis |
string |
EU1 |
defines the time discretization to be used. Possible values are
EU1 for first order explicit Euler-Method, AB2 for second order explicit Adams-Bashforth-Method,
RK2 for second order Runge-Kutta-method and RK3 for third order Runge-Kutta-method.
Remark: The Runge-Kutta-method of third order is only available for the time derivatives in
equations (![[*]](file:/usr/share/latex2html/icons/crossref.png) ) and ( ) and (![[*]](file:/usr/share/latex2html/icons/crossref.png) ),
setting TimeDis to RK3 results in application of the Runge-Kutta-method of second order to
the other time derivatives ),
setting TimeDis to RK3 results in application of the Runge-Kutta-method of second order to
the other time derivatives |
| ConvectiveTerms |
string |
VONOS |
defines the discretization scheme to be used for the convective terms.
Possible values are DC (Donor-Cell, 1st/2nd order), HLPA (Hybrid Linear-Parabolic Approximation, 1st/2nd order),
QUICK (Quadratic Upwind Interpolation for Convective Kinematics, 2nd order), SMART
(Sharp And Monotonic Algorithm for Realistic Transport, 2nd order) and VONOS
(Variable-Order Non-Oscillatory Scheme, 2nd order) |
| PoissonSolver |
string |
BiCGStab |
set the method for solution of the linear system arising from
discretization of the pressure poisson equation. Possible values are SOR, SSOR, RedBlack, 8ColorSOR, 8ColorSSOR and
BiCGStab (preconditioned with Jacobi-Method) |
| alpha |
double |
1.0 |
defines the blending parameter 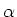 in the convex combination of
the central difference/upwind discretization of the convective terms of in the convex combination of
the central difference/upwind discretization of the convective terms of 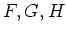 . .
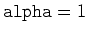 means pure upwind and means pure upwind and
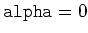 results in pure central difference discretization results in pure central difference discretization |
| alphaTC |
double |
1.0 |
same as alpha, but for convective terms in the transport
equation used for computation of temperature and scalars |
| Parameters for the linear solver |
| |
|
|
|
| itermax |
int |
100 |
defines the maximal number of iterations in the linear solver
(BiCGStab,SOR, SSOR etc.) |
| eps |
double |
0.001 |
defines the stopping criterion for the iterations in the linear solver.
The parameter eps is the upper bound for the residual of the poisson equation, i.e. the iterations
are stopped if
Here, 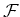 is the set of all fluid cells in is the set of all fluid cells in 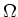 and and
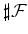 is the cardinality of is the cardinality of 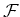 . .
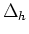 and and 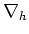 denote the discrete Laplacian and gradient operator. denote the discrete Laplacian and gradient operator. |
| omega |
double |
1.7 |
sets the relaxation parameter for the SOR-type solvers |
| Boundary conditions |
| |
|
|
|
| periodboundx |
|
|
sets periodic boundary conditions in direction of 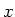 -coordinate -coordinate |
| periodboundy |
|
|
same as periodboundx only for the 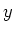 -coordinate-direction -coordinate-direction |
| periodboundz |
|
|
same as periodboundx only for the 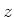 -coordinate-direction -coordinate-direction
|
|
|
|
|
![]() .
.
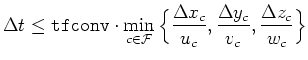
![$\displaystyle \Delta t\leq{\tt tfdiff}\min_{\nu\in{\cal N},c\in{\cal F}}
\Big[\...
...1{{\Delta x_c}^2}+\frac1{{\Delta y_c}^2}+\frac1{{\Delta z_c}^2}\Big)\Big]^{-1} $](img194.png)