Adaptive wavelet solver for the Navier-Stokes Equation

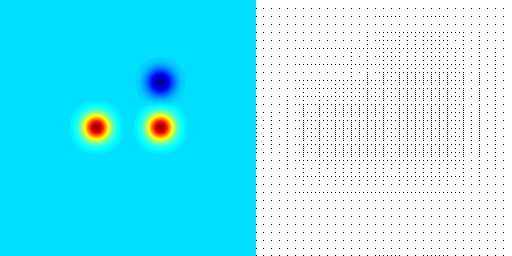
Merging of Vortices

The initial configuration are three vortices. Under the influence of the velocity field they induce, they start to rotate around each other and then to merge.

• Domain: $[0,1]\times[0,1]$ , time: $0.0\dots80.0\ \text{units}$
• Maximum velocity: $0.07$ , Re: $55000$
• Time step: $5 \cdot 10^{-3}$ , finest mesh size: $1/2048$

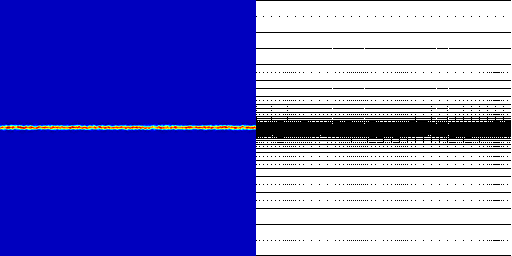
The left figure shows the vorticity and the right figure shows the adaptive grid associated to the current adaptive basis

Merging of vortices

Numerical Experiment: 2D Mixing Layer

The initial configuration are two flows in the upper and lower half of $[0,1]\times[0,1]$ with opposite sign. The vorticity in the interfacial layer is randomly perturbated. Kelvin-Helmholtz instabilities lead to the development of vortices which in a later stage roll-up and merge. This is a nice example for the tendency of 2D turbulence to transfer energy from small to large scales. This leads to a fast decrease of the complexity of the flow and to a decrease of the number of degrees of freedom required for an accurate numerical simulation.

• Domain: $[0,1]\times[0,1]$ , time: $0.0\dots80.0\ \text{units}$
• Minimum/maximum velocity: $\pm 0.018$ , Re: $15000$
• Time step: $5 \cdot 10^{-3}$ , finest mesh size: $1/2048$

2D mixing layer

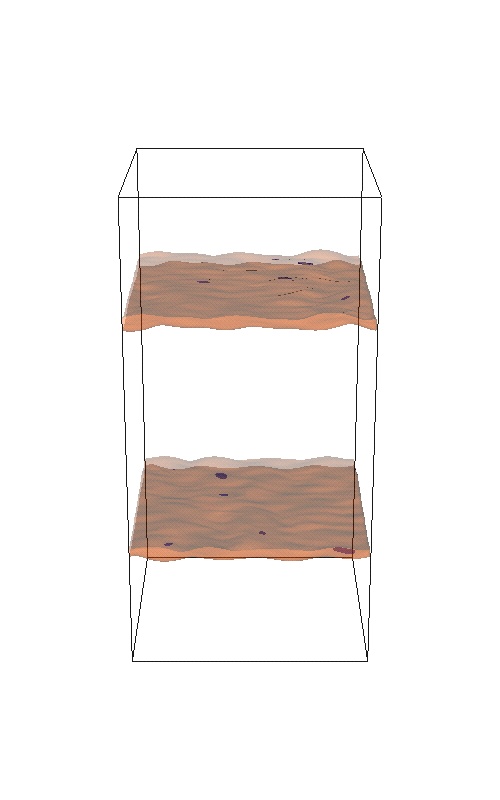
Numerical Experiment: 3D Mixing Layer

The initial configuration is the 3D analogue of the 2D mixing layer. However, due to the 3D character there is an energy transfer from large to small scales which leads to an increase of the complexity of the flow.

• Domain: $[0,1]\times[0,2]\times[0,1]$ , time: $0.0\dots46.0\ \text{units}$
• Minimum/maximum velocity: $\pm 0.018$ , Re: $3750$
• Time step: $2 \cdot 10^{-2}$ , finest mesh size: $1/512$
• Number of DOF from $1$ to $2$ million

3D mixing layer

Author: Frank Koster