Project Mathematik für maschinelle Lernmethoden für Graph-basierte Daten mit integriertem Domänenwissen

Derzeit erleben wir einen weltweiten Siegeszug des Maschinellen Lernens (ML), insbesondere der tiefen neuronalen Netze (TNNs), der sich nicht nur auf verschiedene Anwendungsbereiche, sondern auch auf mathematische Themen wie inverse Probleme auswirkt. Große vorhandene Datenmengen und die deutlich gestiegene Computerleistung machen die Anwendung und das erfolgreiche Training tiefer neuronaler Netzwerke möglich. Dabei wurden bisher meist sogenannte „end-to-end“-Lernansätze verwendet, für die in der Regel sehr große Mengen strukturierter Daten notwendig sind. Dies führt dazu, dass diese Ansätze in vielen realen Anwendungsfällen aus den Naturwissenschaften, der Medizin und der Industrie nur bedingt einsetzbar sind. Denn meist sind nur komplexe und heterogene Datenbestände vorhanden, und die Generierung zuverlässiger Daten ist teuer und aufwändig. Hier setzt MaGriDo an und verfolgt das Ziel, existierendes Domänenwissen zu integrieren, um so insbesondere die Anzahl der notwendigen Daten für ausreichend genaue TNNs substantiell zu reduzieren.

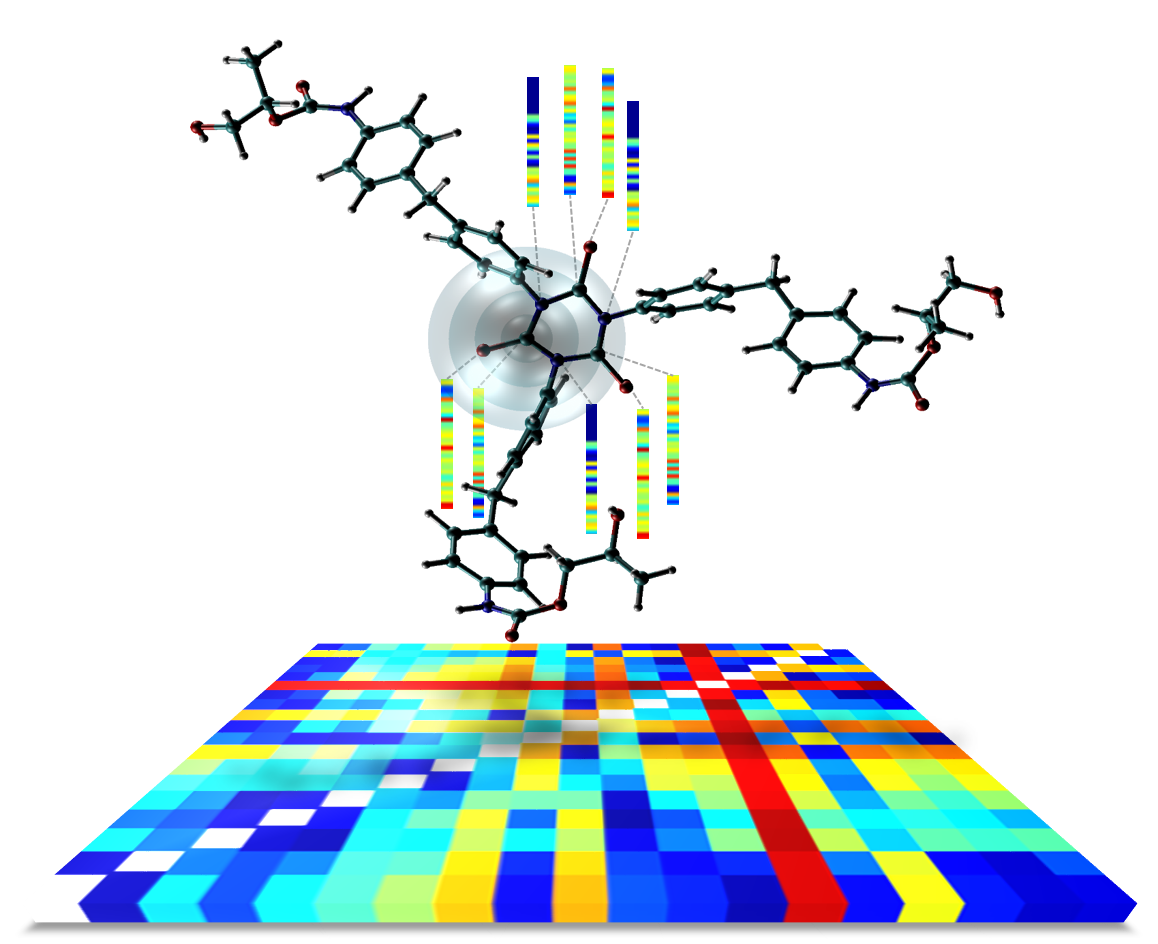
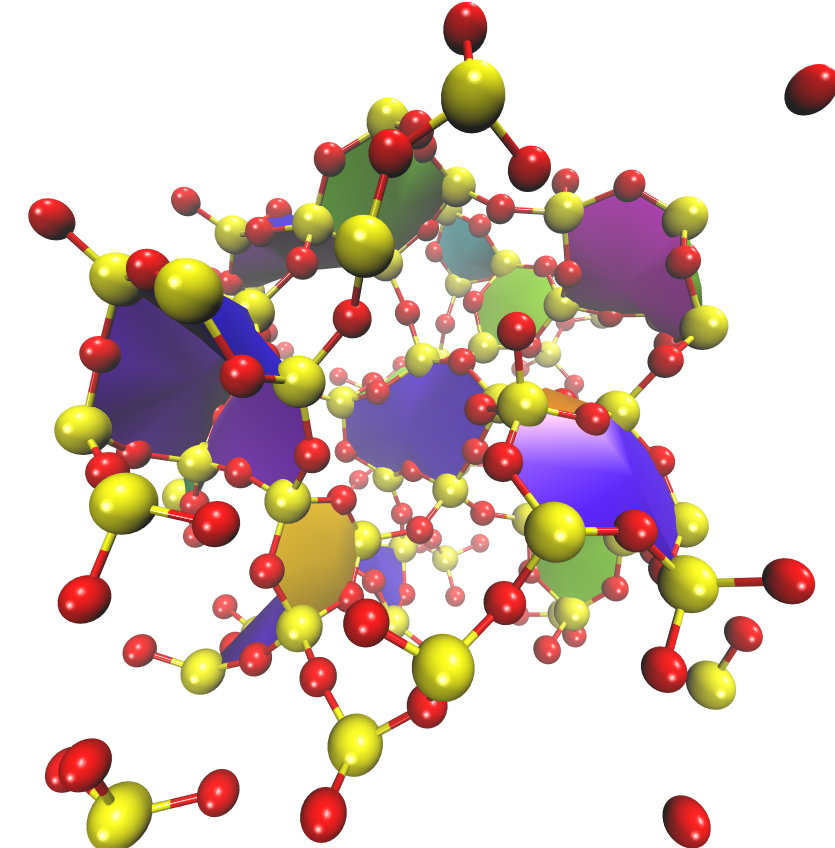
Im Fokus von MaGriDo stehen praxisrelevante Problemstellungen aus den Materialwissenschaften, vor allem Polymere und Gläser. Zum Beispiel werden Polyurethan-Lacke seit über 60 Jahren für Automobile, Möbel oder Parkett genutzt. Abhängig von den Anforderungen kommen mehrere Grundstoffen zum Einsatz. Gerade durch die große Variationsmöglichkeit dieser Komponenten sind die Eigenschaften (Härte, Lösungsmittelbeständigkeit, Kratzfestigkeit, Hydrolysebeständigkeit, Glanz) wie in einem Baukastensystem einstellbar. Die Vorhersage der Eigenschaften basiert bisher zum großen Teil auf Versuch-und-Irrtum-Methoden und auf jahrelanger Erfahrung der Hersteller und Anwender. Ein weiteres Beispiel ist die Herstellung von Gläsern. Auch hier gibt es eine Vielzahl einsetzbarer Grundstoffen und eine große Variationsmöglichkeit der Prozessparameter. Für diese Probleme sollen Lernverfahren weiterentwickelt, untersucht und auf Daten der Praxispartner angewendet werden. Ein Schwerpunkt liegt auf Regressionsproblemen.

Zielsetzung

Ziel von MaGriDo ist es, TNNs für Problemstellungen aus der Industrie (weiter) zu entwickeln und zu analysieren, die es erlauben, existierendes Domänenwissen in die Architektur der Netzwerke einzubauen. Solch ein hybrider Ansatz kann die komplementären Stärken von „end-to-end“-Lernansätzen und „a-priori-Modellen/Regeln“ nutzbar machen. Dieses Vorgehen verspricht effizientere Lösungen für viele Anwendungsfelder. Beispielsweise reduziert sich die benötigte Datenmenge, oder die Vorhersagen des ML-Modells sind konsistent zum vorhandenen Wissen.

Der Schwerpunkt der Forschung und Entwicklung in MaGriDo wird auf sogenannte Graphnetzwerke gelegt, da üblicherweise komplexe Systeme sehr gut als Zusammensetzungen von Entitäten und deren Wechselwirkungen repräsentiert werden können. Diese enthalten zum Beispiel konventionelle Fully-Connected-NN, Convolution-NN und Recurrent-NN als Spezialfälle, lassen sich auf relationalen Strukturen angewenden und ermöglichen eine hierarchische Prozessierung der Eingabedaten. Mathematische Aspekte

Die mathematischen Untersuchungen im Vorhaben sollen letztlich zum besseren Verständnis der Architektur von TNNs beisteuern. Die mathematischen Beiträge des Vorhabens umfassen

  • die Untersuchung und Erarbeitung einer Expressivitätsanalyse für Graphnetzwerke,
  • die Erweiterung von Interpretierbarkeitsalgorithmen und deren Theorie auf Graphnetzwerke,
  • die Untersuchung effizienter Lernverfahren für das Training von Graphnetzwerken,
  • die Betrachtung von Graphnetzwerkarchitektur, Regularisierung und Optimierungsverfahren,
  • die strukturierte Integration von Domänenwissen durch geeignete mathematische Formalismen,
  • die Erarbeitung mathematischer Konzepte zum Transferlernen und aktiven Lernen,
  • die Erarbeitung und Untersuchung systematisch verbesserbarer Wechselwirkungspotentiale,
  • die Untersuchung generativer Graphnetzwerke.

Die mathematischen Methoden und Erkenntnisse von MaGriDo sind nicht auf das Feld der Materialwissenschaften beschränkt. Graphnetzwerke sind auf viele andere Anwendungsfelder übertragbar, beispielsweise um Wissengraphen in der Systembiologie und Biomedizin in TNNs einzubinden.

Projektpartner

Industriepartner

MaGriDo wird im Rahmen des Programms »Mathematik für Innovationen« vom Bundesministerium für Bildung und Forschung (BMBF) unter der Projektkennziffer 05M20PDB gefördert.