Modeling and Simulation of Additive Manufacturing Processes

Overall Research Goals

Additive manufacturing (AM) has gained more and more momentum in recent years, but has yet to fullfil the promise of becoming the widely used break-through-technology that will revolutionize manufacturing in the 21st century. Despite all the advantages, such as the high degree of design freedom and the shortened production time for highly complex parts, additively manufactured components are still hardly used in safety-relevant areas. This is due to the fact that, compared to conventional processes such as milling, the processes are significantly more complex and the material quality of the manufactured component cannot be predicted with certainty. Time-consuming and costly quality control requirements prevent the widespread use of AM. These issues can in principle be overcome by advanced modeling and simulation of the manufacturing process which will then allow to optimize the process.

For the design of AM components and for the simulation of a Laser Powder Bed Fusion (LPBF) process, solutions are offered by various software vendors, such as Siemens, Altair or ANSYS. However, these solutions reflect the low level of maturity of the still young 3D printing technologies. Their capabilities are not sufficient to obtain accurate process control. In order to be able to obtain the required accuracy, a multiscale and multidisciplinary approach is required that combines experimental and theoretical work with computer simulations on multiple length scales.

The simulation of the LPBF process involves various challenges. Obviously, the domain evolves during the process by adding additional layers of powder. Moreover, multiple phase changes need to be resolved, from powder to liquid and from liquid to solid, since a direct conversion from powder to solid is not possible. Material phases form and transform during subsequent laser passes. Furthermore, this extremly complex environment is truely a multiscale process. The laser heat source is highly localized (about 100 micron) and in case of AMB laser sources may require the resolution of even further details. Yet, the printed product is typically on the scale of decimeters and scale separation in LPBF is not given due to the intermediate powder bed layer scale. Similarly, a large range of time scales is involved and needs to be resolved appropriately. While local melting and solidification takes place within milliseconds, the complete manufacturing of a final part may require multiple days. Finally, we need to deal with all of these challenges on computational domains which shape and topology may be extremely complex and change substantially over time.

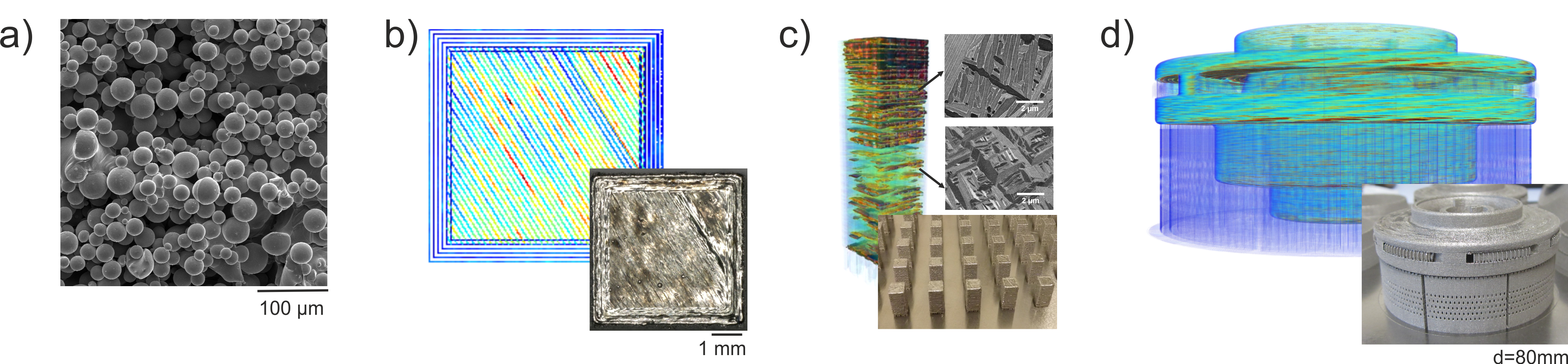Examples for the multiscalarity of additive manufacturing: a) raw powder, b) melt pool monitoring (MPM) data for a single melted layer and the corresponding light optical image; c) MPM data of a small cuboid exhibiting different microstructures; d) MPM data and image of a larger component. (source: DLR)

Overall, the LPBF process constitutes a multi-physics problem, where the largest temperature gradients are induced by the moving and highly localized laser beam which in turn yield the phase changes in close vicinity of the beam. The involved phase changes are typically modeled by

$\rho c \frac{\partial T}{\partial t} + \rho L \frac{\partial f_{pc}}{\partial t} - \nabla \cdot (k \nabla T) = Q$

where $\rho$, $c$, $L$ and $f_{pc}$ denote density, specific heat capacity, latent heat and a phase-change function, $k$ is the thermal conductivity, $Q$ is the heat source and $T$ the temperature. Due to the significant changes in temperature during the process, some regions in the domain expand, while some others contract which leads to residual stresses in the part and potentially render the product not fit-for-use in safety-relevant applications. These stresses are computed via a quasi-static mechanical model given by

$\nabla \cdot \sigma + f - f_{th} = 0$

where $f_{th}$ denotes the thermal load induced by the temperature field $T$.

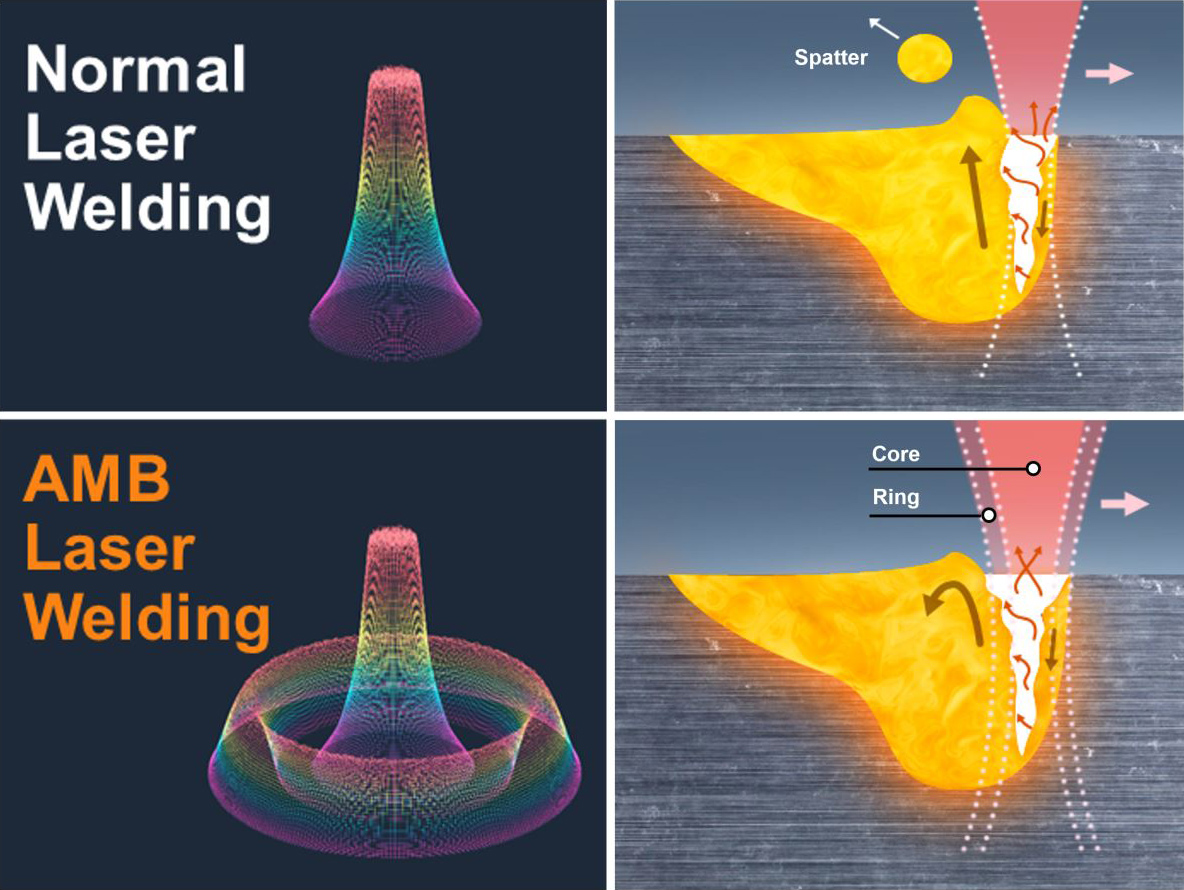
The simulation environment to be developed is intended to cover all relevant scales in the long term from the powder level to the entire component. In order to build up a process simulation tool that can be expanded and is suitable for research, a high degree of flexibility in the modeling is important. This will also include the implementation of variable beam profiles such as e.g. from new Ringmode-lasers (Figure 1) that are not yet standard in AM processes. At the same time, as much as possible should be built on existing simulation modules. Therefore, a meshfree partition of unity method (PUM), a generalization of the finite element method (FEM), with which multiscale partial differential equations can be solved on complex geometries, offers an ideal basis for such a development. In contrast to classical FEM, a meshing of the simulation domain can be omitted. Local refinements and free surfaces can be easily represented. Finally, the basis functions of the PUM, from which the solution is constructed, can be enriched by domain knowledge, experimental results, AI building blocks or further simulation results. Thus, the multiscale underlying additive manufacturing can be achieved by local refinements in the PUM, enrichment of the basis functions, and by uni- or bidirectional co-simulation with other simulation tools. As a first step in the course of the project, we want to answer the question how the heat input by the lasers at powder level is transferred to the overall component.