Practical Lab WS 20/21 Practical Lab Numerical Simulation
Shape optimization with FEniCS
Elastic shape optimization aims at the computation of the optimal shape of an elastic object, for example the shape with the smallest deformation, given certain material properties, volume, and external forces. In the lab we consider
- the partial differential equations of linearized and nonlinear elasticity,
- the description of variable shapes with parametrized transformations, phase field functions or as level sets,
- the formulation of the shape optimization problem as an minimization problem with a partial differential equation as a constraint,
- the computation of the gradient of the target functional with respect to shape variations,
- and the implementation of suitable optimization strategies.
The implementation will be done in Python using the FeniCS platform.
We will have one (probably virtual) meeting per week, the time will be discussed before the term starts. The meetings will alternate between introducing new programming tasks, discussing problems and evaluating solutions. Programming can be done alone or in groups of up to three people.
The course is open for Bachelor (P2E1) ans Master (P4E1) students. Most of the meetings will be scheduled for all participants, there will be some additional meetings with basics for Bachelor students or additional content for Master students. The programming tasks for the two groups will differ in complexity and depth, and can be adapted to different levels of previous knowledge.
For simplicity there is only one eCampus course, please enroll for more information.
Example
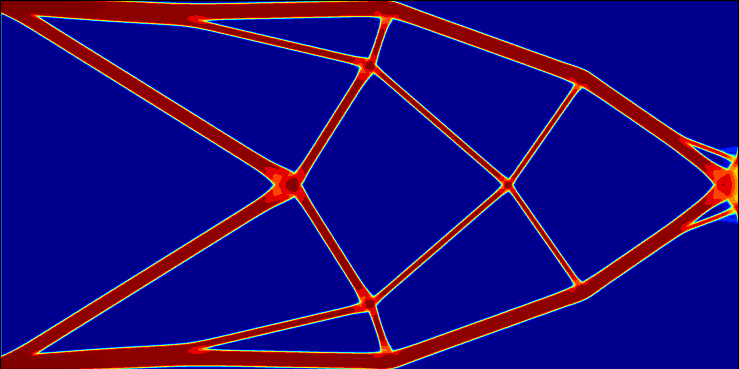
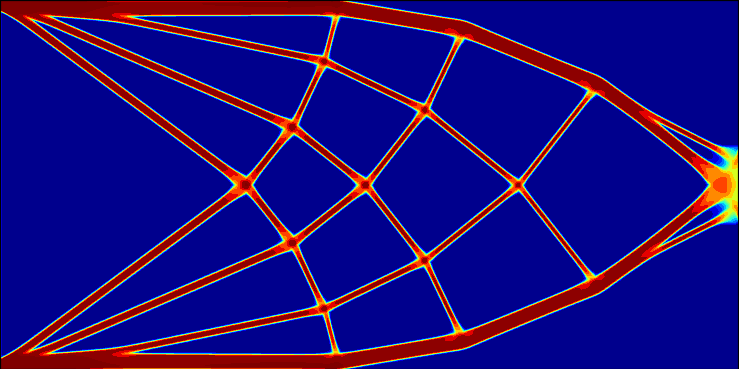
We consider a cantilever that is fixed to the wall on the left end and carries a weight on the right end. The cantilever deforms elastically (it bends downwards). Now the question of shape optimization is: Which shape should the cantilever have, so that it deforms as little as possible, while using als little material as possible?
To this end we have to describe the shape by a function. We can, for example, use a function that is equal to 1 inside the cantilever, equal to -1 outside the cantilever, with a smooth transition region in between.
In addition, we have to formulate the functional we want to optimize. In our example, this might be a weighted sum of displacement of the tip of the cantilever, the volume and the surface of the cantilever.
The following images show the result of a shape optimization algorithm, with different factors in front of the surface of the shape. Decreasing importance of the surface results in finer structures in the optimal shape. (red = 1 = cantilever, blue = -1 = void).