Staff Dr. Martin Lenz

Address:
Institut für Numerische Simulation
Endenicher Allee 60
53115 Bonn
Phone: +49 228 73-3416
Office: EA60 2.037
E-Mail: ed tod nnob-inu tod sni ta znel tod nitrama tod b@foo tod de

Teaching

Summer semester 2023

Winter semester 2022/23

See teaching activities of the whole group.

Research Projects

Current

Numerical optimization of shape microstructures

Project C06, DFG SFB 1060.

Show description. Homepage.

Completed

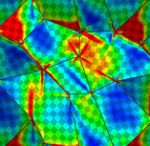
Mathematical modeling and simulation of microstructured magnetic-shape-memory materials

Project A6, DFG priority program 1239.

Show description. Homepage.

Publications

  1. Microstructure of macrointerfaces in shape-memory alloys. S. Conti, M. Lenz, M. Rumpf, J. Verhülsdonk, and B. Zwicknagl. submitted, 2022. BibTeX
  2. Geometry of martensite needles in shape memory alloys. S. Conti, M. Lenz, N. Lüthen, M. Rumpf, and B. Zwicknagl. C. R. Math. Acad. Sci. Paris, 358(9-10):1047–1057, 2020. BibTeX DOI arXiv
  3. A posteriori modeling error estimates in the optimization of two-scale elastic composite materials. S. Conti, B. Geihe, M. Lenz, and M. Rumpf. ESAIM: Mathematical Modelling and Numerical Analysis, 52(4):1457–14761, July–August 2018. BibTeX PDF DOI arXiv
  4. Homogenization in magnetic-shape-memory polymer composites. S. Conti, M. Lenz, M. Pawelczyk, and M. Rumpf. In V. Schulz and D. Seck, editors, Shape Optimization, Homogenization and Optimal Control : DFG-AIMS workshop held at the AIMS Center Senegal, March 13-16, 2017, pages 1–17. Springer International Publishing, Cham, 2018. BibTeX DOI
  5. Hysteresis in magnetic shape memory composites: modeling and simulation. S. Conti, M. Lenz, and M. Rumpf. J. Mech. Phys. Solids, 89:272–286, 2016. BibTeX PDF DOI arXiv
  6. Risk averse elastic shape optimization with parametrized fine scale geometry. B. Geihe, M. Lenz, M. Rumpf, and R. Schultz. Mathematical Programming, 141(1-2):383–403, 2013. BibTeX PDF DOI
  7. Modeling and simulation of large microstructured particles in magnetic-shape-memory. S. Conti, M. Lenz, and M. Rumpf. Advanced Engineering Materials, 14(8):582–588, 2012. BibTeX PDF DOI
  8. A convergent finite volume scheme for diffusion on evolving surfaces. M. Lenz, S. F. Nemadjieu, and M. Rumpf. SIAM Journal on Numerical Analysis, 49(1):15–37, 2011. BibTeX PDF DOI
  9. Macroscopic behaviour of magnetic shape-memory polycrystals and polymer composites. S. Conti, M. Lenz, and M. Rumpf. In 7th European Symposium on Martensitic Transformations and Shape Memory Alloys, volume 481–482 of Materials Science and Engineering: A, 351–355. 2008. BibTeX PDF DOI
  10. Finite volume method on moving surfaces. M. Lenz, S. F. Nemadjieu, and M. Rumpf. In R. Eymard and J.-M. Hérald, editors, Finite Volumes for Complex Applications V, 561–576. Wiley, 2008. BibTeX PDF
  11. Modeling and simulation of magnetic shape-memory polymer composites. S. Conti, M. Lenz, and M. Rumpf. Journal of Mechanics and Physics of Solids, 55:1462–1486, 2007. BibTeX PDF DOI
  12. Modellierung und Simulation des effektiven Verhaltens von Grenzflächen in Metalllegierungen. M. Lenz. Dissertation, University Bonn, 2007. BibTeX PDF Read
  13. Multiple scales in phase separating systems with elastic misfit. H. Garcke, M. Lenz, B. Niethammer, M. Rumpf, and U. Weikard. In A. Mielke, editor, Analysis, Modeling and Simulation of Multiscale Problems. Springer, 2006. BibTeX PDF Publisher
  14. Numerical methods for fourth order nonlinear degenerate diffusion problems. J. Becker, G. Grün, M. Lenz, and M. Rumpf. Applications of Mathematics, 47(6):517–543, 2002. BibTeX DOI
  15. A finite volume scheme for surfactant driven thin film flow. G. Grün, M. Lenz, and M. Rumpf. In R. Herbin and D. Kröner, editors, Finite Volumes for Complex Applications III, 567–574. Hermes Penton Sciences, 2002. BibTeX PDF
  16. Finite Volumen Methoden für degenerierte parabolische Systeme – Ausbreitung eines Surfactant auf einem dünnen Flüssigkeitsfilm. M. Lenz. Diploma thesis, University Bonn, 2002. BibTeX PDF
  17. A procedural interface to hierarchical grids. T. Geßner, B. Haasdonk, R. Kende, M. Lenz, R. Neubauer, M. Metscher, M. Ohlberger, W. Rosenbaum, M. Rumpf, R. Schwörer, M. Spielberg, and U. Weikard. Technical Report, SFB 256, University Bonn, 1999. BibTeX PDF Link