Research Group of Prof. Dr. Daniel Peterseim
This is a former research group of the institute. This page is no longer maintained.
Research Projects
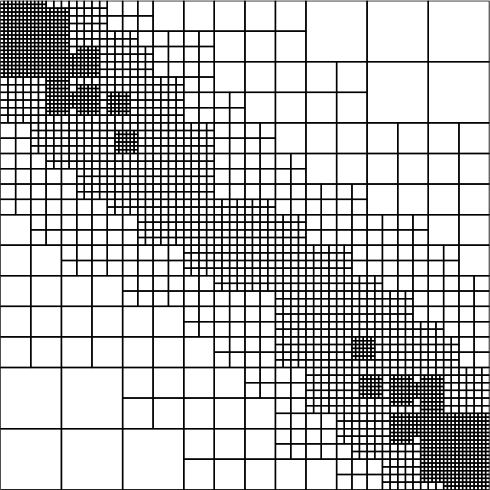
Adaptive Algorithms for Partial Differential Equations

Adaptive isogeometric modeling of propagating strong discontinuities in heterogeneous materials

Linear and Nonlinear Eigenvalue Problems
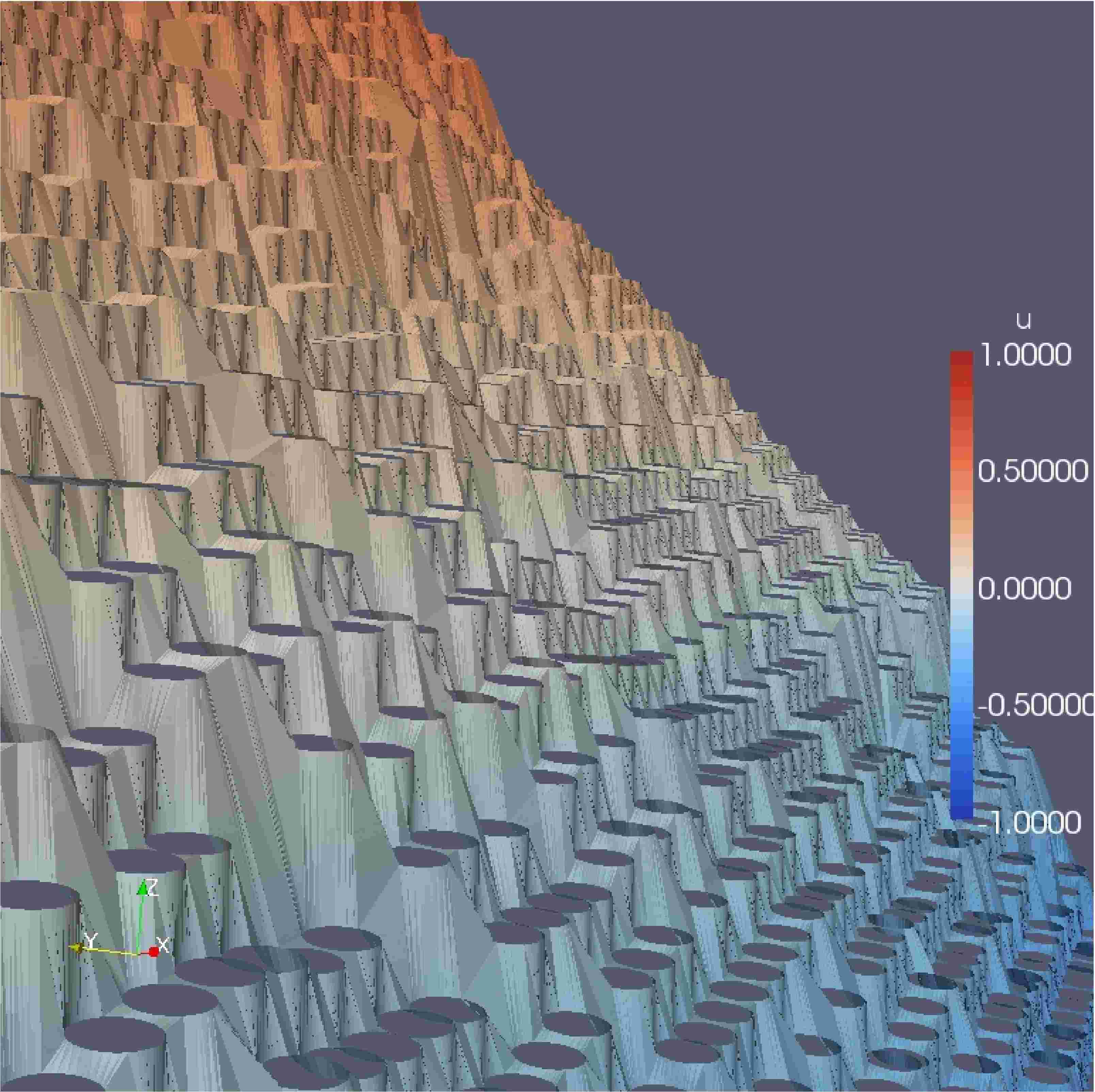
Modeling and Simulation of Composite Materials

Numerical Homogenization

Wave Propagation and Scattering
The numerical simulation of acoustic or electromagnetic high-frequency wave propagation is still among the most challenging tasks of computational partial differential equations. The highly oscillatory nature of the solution plus a wave number dependent pollution effect put very restrictive assumptions on the smallness of the underlying mesh. Typically, this condition is much stronger than the minimal requirement for a meaningful representation of highly oscillatory functions from approximation theory.
We develop pollution-free methods for homogeneous and heterogeneous frequency domain models as well as adaptive and parallel solution strategies in the time-domain. We expect that these techniques will be very useful in the context of parameter studies and inverse problems and we aim at their transfer to geophyiscal and medical applications.