Research Group of Prof. Dr. Daniel Peterseim
This is a former research group of the institute. This page is no longer maintained.
Research Projects
Adaptive Algorithms for Partial Differential Equations

Adaptive isogeometric modeling of propagating strong discontinuities in heterogeneous materials

Linear and Nonlinear Eigenvalue Problems
Our new techniques for computational homogenization for linear elliptic problems yield promising results also for elliptic eigenvalue problems with possibly very rough data. Those results show that numerical upscaling may be performed in such a way that the homogenized (effective) operator preserves small eigenvalues extremely accurate. This observation has surprising applications, e.g., the computation of ground states of Bose-Einstein condensates in quantum chemistry. This research is continued in the context of non-linear Schrödinger equations and other classes of linear and nonlinear (polynomial) eigenvalue problems, for example the mechanical analysis of damped vibrating structures.
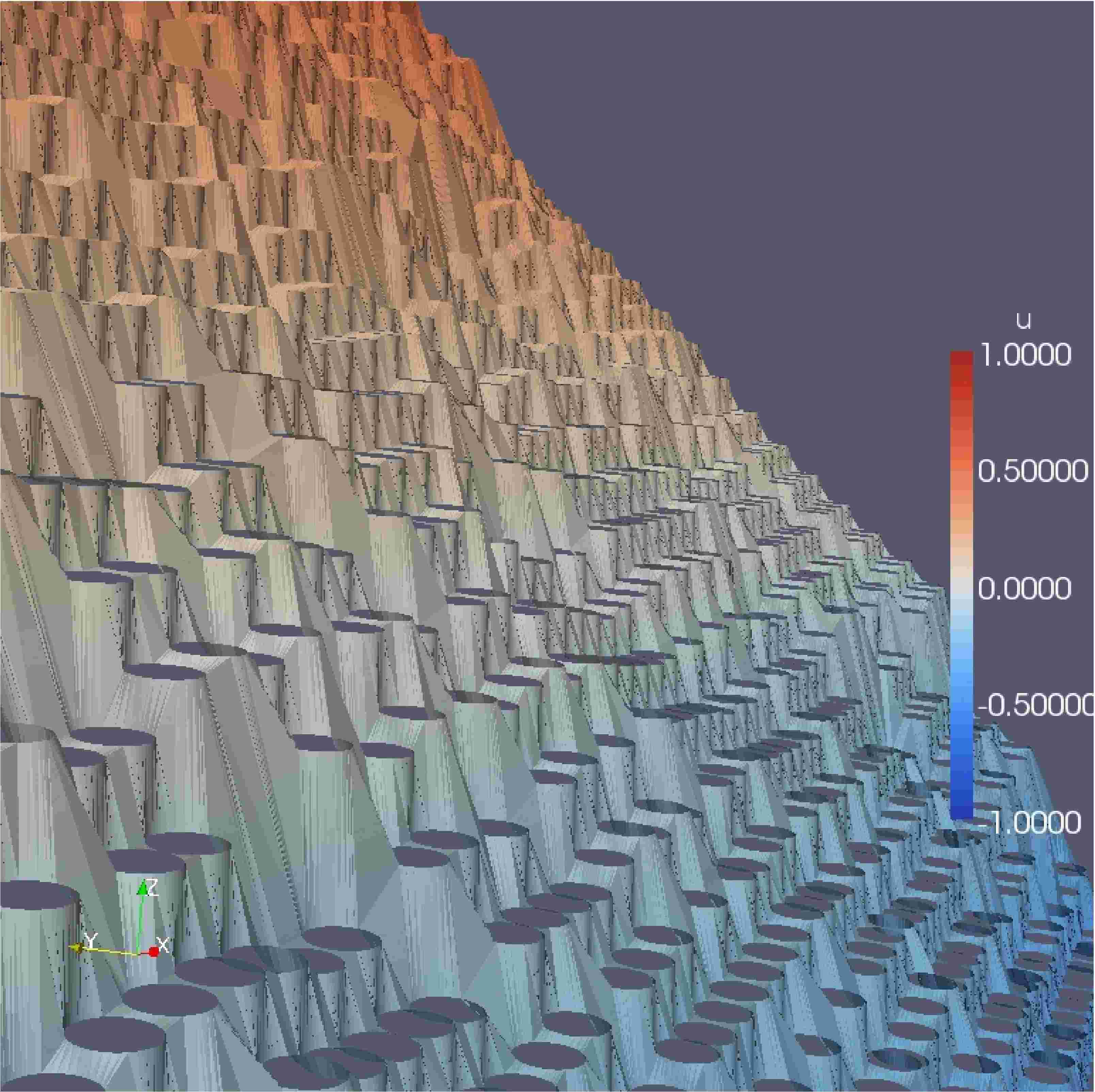
Modeling and Simulation of Composite Materials

Numerical Homogenization
