Staff Dr. Behrend Heeren

Mr. Heeren is now at Nexocraft. This page is no longer maintained.

E-Mail: ed tod nnob-inu tod sni ta nereeh tod dnerheba tod b@foo tod de

Teaching

Summer semester 2020

Winter semester 2019/20

Winter semester 2018/19

See teaching activities of the whole group.

Completed Research Projects

4D structural analysis of the sugar beet geometry

Project D4, BMBF competence network.

Show description. Homepage.

A Functional Map Approach to Shape Spaces

German-Israeli Foundation.

Show description.

Discrete Riemannian calculus on shape space

Project C05, DFG SFB 1060.

Hide description. Homepage.

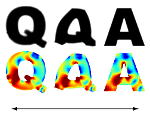
The theory of shape spaces in vision is linked both to concepts from geometry and from physics. The flow of diffeomorphism approach and the optimal transportation approach are prominent examples for Riemannian metric structures on the space of shapes, intensively studied in the last decade. In general, the numerical realization of the underlying infinite dimensional Riemannian calculus poses enormous computational challenges. In this project we propose suitable time and space discrete approximations. They will be based on optimal matching deformations, which are significantly cheaper to compute but by construction non-Riemannian. We will also study abstract concepts of transportation between metric measure spaces with particular focus on spaces consisting only of a fixed number of points.

In the time discrete calculus a discrete path energy is defined as the sum of pairwise deformation energies along a discrete path. Using a variational approach one can deduce from this step by step a discrete logarithm, a discrete exponential map, a discrete parallel transport, a discrete Levi-Civita connection, and finally a discrete Riemannian curvature tensor. This concept will be applied and analyzed in particular for the flow of diffeomorphism and the optimal transportation approach.

Furthermore, with respect to a spatially discrete covering of shape space, the approach of deformation based shape dissimilarities will be combined with the diffusion map paradigm expedited by Coifman and coworkers to introduce physically sound and computationally efficient approximations of metric structures on shape spaces.

Overall, we aim at combining methods from geometry, stochastic analysis and numerics to advance theory in computer vision and explore new applications with efficient computational tools.

Geodesic Paths in Shape Space

Project 5, FWF NFN S117.

Show description. Homepage.

Publications

  1. Consistent curvature approximation on Riemannian shape spaces. A. Effland, B. Heeren, M. Rumpf, and B. Wirth. IMA J. Numer. Anal., 42(1):78–106, 2022. BibTeX DOI arXiv
  2. Shape space - a paradigm for character animation in computer graphics. B. Heeren and M. Rumpf. Technical Report 07, Mathematisches Forschungsinstitut Oberwolfach, 2020. BibTeX DOI
  3. Statistical shape analysis of tap roots: a methodological case study on laser scanned sugar beets. B. Heeren, S. Paulus, H. Goldbach, H. Kuhlmann, A.-K. Mahlein, M. Rumpf, and B. Wirth. BMC Bioinformatics, 21:335, 2020. BibTeX DOI PDF
  4. Discrete Riemannian calculus on shell space. B. Heeren, M. Rumpf, M. Wardetzky, and B. Wirth. In R. Nochetto and A. Bonito, editors, Geometric Partial Differential Equations - Part I, volume 21 of Handbook of Numerical Analysis, pages 621–679. Elsevier, 2020. BibTeX DOI
  5. Geometric optimization using nonlinear rotation-invariant coordinates. J. Sassen, B. Heeren, K. Hildebrandt, and M. Rumpf. Computer Aided Geometric Design, 77:101829, 2020. BibTeX DOI arXiv
  6. Elastic correspondence between triangle meshes. D. Ezuz, B. Heeren, O. Azencot, M. Rumpf, and M. Ben-Chen. Comput. Graph. Forum, 38(2):121–134, 2019. presented at EUROGRAPHICS 2019. BibTeX DOI
  7. Variational time discretization of Riemannian splines. B. Heeren, M. Rumpf, and B. Wirth. IMA J. Numer. Anal., 39(1):61–104, 2018. BibTeX PDF arXiv
  8. Principal geodesic analysis in the space of discrete shells. B. Heeren, C. Zhang, M. Rumpf, and W. Smith. Comput. Graph. Forum, 37(5):173–184, 2018. BibTeX PDF DOI
  9. Working memory capacity and the functional connectome - insights from resting-state fMRI and voxelwise eigenvector centrality mapping. S. Markett, M. Reuter, B. Heeren, B. Lachmann, B. Weber, and C. Montag. Brain Imaging and Behavior, 12(1):238–246, 2018. BibTeX
  10. Optimization of the branching pattern in coherent phase transitions. P. W. Dondl, B. Heeren, and M. Rumpf. C. R. Math. Acad. Sci. Paris, 354(6):639–644, 2016. BibTeX DOI arXiv
  11. Numerical Methods in Shape Spaces and Optimal Branching Patterns. B. Heeren. PhD thesis, University of Bonn, 2016. BibTeX
  12. Splines in the space of shells. B. Heeren, M. Rumpf, P. Schröder, M. Wardetzky, and B. Wirth. Comput. Graph. Forum, 35(5):111–120, 2016. BibTeX PDF
  13. Voxelwise eigenvector centrality mapping of the human functional connectome reveals an influence of the catechol-o-methyltransferase val158met polymorphism on the default mode and somatomotor network. S. Markett, C. Montag, B. Heeren, R. Sariyska, B. Lachmann, B. Weber, and M. Reuter. Brain Structure and Function, 221:2755–2765, 2016. BibTeX DOI
  14. Shell PCA: statistical shape modelling in shell space. C. Zhang, B. Heeren, M. Rumpf, and W. Smith. In Proc. of IEEE International Conference on Computer Vision, 1671–1679. 2015. BibTeX PDF DOI
  15. Exploring the geometry of the space of shells. B. Heeren, M. Rumpf, P. Schröder, M. Wardetzky, and B. Wirth. Comput. Graph. Forum, 33(5):247–256, 2014. BibTeX PDF
  16. Discrete geodesic regression in shape space. B. Berkels, P. T. Fletcher, B. Heeren, M. Rumpf, and B. Wirth. In Proc. of International Conference on Energy Minimization Methods in Computer Vision and Pattern Recognition, volume 8081 of Lecture Notes in Computer Science, 108–122. Springer, 2013. BibTeX PDF DOI
  17. Time-discrete geodesics in the space of shells. B. Heeren, M. Rumpf, M. Wardetzky, and B. Wirth. Comput. Graph. Forum, 31(5):1755–1764, 2012. BibTeX PDF DOI
  18. Geodätische im Raum von Schalenformen. B. Heeren. diploma thesis, Institut für Numerische Simulation, Universität Bonn, 2011. BibTeX