Research Group of Prof. Dr. Martin Rumpf
Research Projects
Current



Numerical optimization of shape microstructures
Project C06, DFG SFB 1060.
Completed

4D structural analysis of the sugar beet geometry
Project D4, BMBF competence network.
Anisotropic Curvature Flows in Surface Modeling
Mathematical modeling and simulation of microstructured magnetic-shape-memory materials
Project A6, DFG priority program 1239.
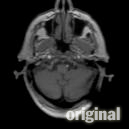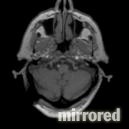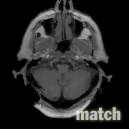
Morphological Non-Rigid Registration
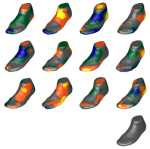
Multi-Scale Shape Optimization under Uncertainty
Our project deals with stochastic shape optimization for elastic materials where stochasticity enters the problem both via stochastic loading and stochastic geometry. We intend to bring together the analytical treatment of multi-scale problems via homogenization, the reliable numerical solution of PDE problems on complex domains described via level sets or phase field models, and two-stage stochastic programming approaches using different perceptions of risk aversion.
Different concepts of stochastic dominance are becoming increasingly attractive in decision making under uncertainty. They allow for flexible risk aversion via comparison with benchmark random variables. Rather than handling risk aversion in the objective this enables risk aversion in the constraints. In our project this is another conceptual transfer of a paradigm from finite dimensional stochastic programming. Dominance constraints single out subsets of nonanticipative shapes which compare favorably to a chosen stochastic benchmark. The new class of stochastic shape optimization problems we plan to investigate arises by optimizing over such feasible sets.
In many real world applications of stochastic shape optimization such as clothes design a nonanticipative prototype shape has to adapt to an uncertain realization of an elastic body. This is quantifiable with various risk measures which go beyond expected value minimization. We intend to apply a principal component analysis to reduce the computational complexity. Our implementation is based on a phase field description of the prototype shape.
So far we have studied stochastic shape optimization based on a full resolution of the geometry. In this setting topological modification turned out to be crucial which led us to adapting the concept of topological derivatives for stochastic cost functionals. We intend to advance this research in order to include correlation between separate nearby holes.
The same correlations will be studied by a two scale method in which they appear on the micro–scale. We will consider rigorous analysis of this approach and develop an efficient numerical method based on boundary elements on a parametric microscopic shape and macroscopic finite elements. Microstructures will consist of a regular lattice of holes with varying size and orientation. Concrete examples are two shells with perforated connecting material and a hard shell filled with porous material such as bones.

Segmentation with adaptive Level Set methods