Research Group of Prof. Dr. Martin Rumpf
Research Projects
Current


This project will provide robust and flexible tools for the quantitative analysis of shapes in the interplay between applied geometry and numerical simulation. Here, shapes S are curved surfaces which physically represent shell-type geometries, boundary geometries of volumetric physical objects, or material interfaces. In isogeometric analysis one faces a wide range of low- and moderate-dimensional descriptions of complicated and realistic geometries. Thus, the geometric description of shapes will be flexible, ranging from simple piecewise triangular to subdivision-generated spline type surface representations and from explicitly meshed volumes to descriptions via level set or characteristic functions.
The fundamental tool for a quantitative shape analysis is the computation of a distance between shapes SA and SB as objects in a high- or even 1-dimensional Riemannian shape space. Hence, we aim at developing robust models and fast algorithms to compute geodesic paths in shape space. Both for boundary or interface contours and for shell-type surfaces the Riemannian metric will correspond to physical dissipation either of a viscous fluid filling the object volume or due to a visco-plastic behavior of the shells. The key tool of the proposed approach is a coarse time discretization combined with a variational scheme to minimize the underlying least action functional.
For purposes of a geometric analysis not only the resulting value for the distance is of interest. In fact the geodesic paths are natural one parameter families of shapes on which physical simulations and PDE computations can be performed. In case of shapes being represented by shell type surfaces we will apply different approaches:
subdivision surfaces generated from coarse surface triangulations and subdivision-based discrete function spaces as a modeling paradigm associated with spline models in CAD, application of methods from discrete exterior calculus on discrete surfaces to derive robust and geometrically consistent discrete shell models, the approximation of curvature-based functionals in shell models via variational principles on general classes of surface meshes.
In the case of shapes being boundary contours or material interfaces of volumetric objects we aim at representing shapes via characteristic functions, working in the context of variational methods in BV. We will compare this approach with corresponding models based on level set or parametric descriptions. Here, recent results on global minimization of convex functionals on BV and coarse to fine multi-scale relaxation methodologies will be taken into account. For the numerical discretization we aim at using finite elements.

Numerical optimization of shape microstructures
Project C06, DFG SFB 1060.
Completed

4D structural analysis of the sugar beet geometry
Project D4, BMBF competence network.
Anisotropic Curvature Flows in Surface Modeling
Mathematical modeling and simulation of microstructured magnetic-shape-memory materials
Project A6, DFG priority program 1239.
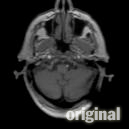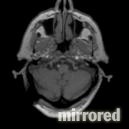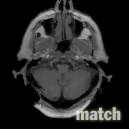
Morphological Non-Rigid Registration
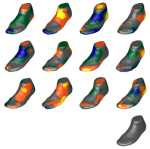
Multi-Scale Shape Optimization under Uncertainty

Segmentation with adaptive Level Set methods