Research Group of Prof. Dr. Martin Rumpf
Research Projects
Current

Three dimensional data is becoming widely available and is required in various applications in science and technology. Developing algorithms for efficiently and robustly analyzing collections of 3D shapes is therefore one of the main problems in geometry processing today. While the problem is widely researched, a thorough understanding of how the space of shapes discretized as triangle meshes should be modeled and treated computationally is still lacking. One of the main challenges is the interplay between the discrete variables representing the triangulation and the continuous variables representing the embedding in three dimensions, which often leads to un-tractable optimization problems. In this proposal we address this challenge by combining recent tools developed for representing correspondences between triangle meshes without explicitly specifying combinatorial changes, with an approach for efficient discrete optimization on the space of shells using geodesic calculus.
The first component allows us to sidestep the explicit representation of the change in the triangulation by using a correspondence between functions spaces defined on the discrete shapes instead of a correspondence between points. Thus, it allows us to represent smooth self-maps as flows of discrete vector fields. The second component allows us to treat discretely various physical energies (such as the elastic energy and bending energy), generating correspondences and new shapes which minimize those energies by computing geodesics on an abstract Riemannian manifold, whose metric is formulated in terms of those energies. Together, the two tools provide a complete description of the shape space of discrete surfaces, allowing us to model both the flow of self-maps of a single surface as well as the flow of deformed surfaces, as geometric problems on an abstract Riemannian manifold with an appropriate metric, which can be addressed using geodesic calculus. This in turn enables us to address computationally previously challenging applications, such as map computation, map improvement, attribute transfer and shape interpolation.


Numerical optimization of shape microstructures
Project C06, DFG SFB 1060.
Completed

4D structural analysis of the sugar beet geometry
Project D4, BMBF competence network.
Anisotropic Curvature Flows in Surface Modeling
Mathematical modeling and simulation of microstructured magnetic-shape-memory materials
Project A6, DFG priority program 1239.
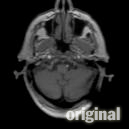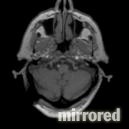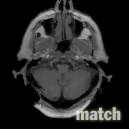
Morphological Non-Rigid Registration
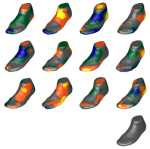
Multi-Scale Shape Optimization under Uncertainty

Segmentation with adaptive Level Set methods